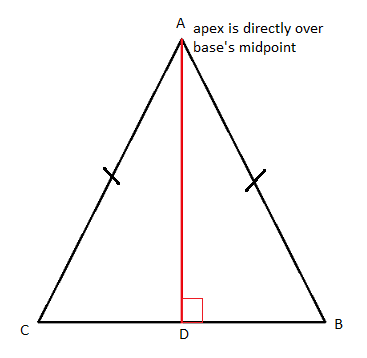
The sum of the lengths of the sides of the isosceles triangle is called its perimeter. Conversely, if the base angles of a triangle are equal, then the triangle is isosceles.” Isosceles triangle theorem states that “In an isosceles triangle, the angles opposite to the equal sides are equal. Therefore ∆ABC is an Isosceles triangle.Īpplying Pythagoras theorem in ∆ABD, we have Top DefinitionsExamplesBritishScientific. If two sides are equal, then the angles opposite to these sides are also equal.įor example, in the following triangle, AB = AC. Now, let us understand the definition of an isosceles triangle.Ī triangle is said to be an Isosceles triangle if its two sides are equal. Also, ancient Babylonian and Egyptian mathematicians were of the know-how on the calculations required to find the ‘ area’ much before the ancient Greek mathematicians started studying the isosceles triangle. The term isosceles triangle is derived from the Latin word ‘īsoscelēs’, and the ancient Greek word ‘ἰσοσκελής (isoskelḗs)’ which means “equal-legged”. The three sides of the triangle above are AB, BC and AC. An exterior angle of a triangle is formed by any side of a triangle and the extension of its adjacent side. The Altitude, AE bisects the base and the apex angle into two equal parts. (geometry) a flat shape with two of its three straight sides the same length. The two angles opposite to the equal sides are equal (isosceles triangle base angle theorem). Scalene triangles can have any combination of side lengths as long as they do not form an equilateral triangle (with all sides equal). This results in all the angles being consequently unequal as well. These angles are also called the interior angles of a triangle. Two equal (congruent) sides in ABC, AB and AC are two congruent sides. A type of triangle in which none of the sides have the same length is called a scalene triangle. The angle formed at A can also be written as ∠BAC. The three angles are the angles made at these vertices, i.e. If and only if one pair of internal angles of two triangles have the same measure as each other, and another pair also have the same measure as each other, the triangles are similar.In the above triangles, the three vertices are A, B and C. Some basic theorems about similar triangles are: The corresponding sides of similar triangles have lengths that are in the same proportion, and this property is also sufficient to establish similarity. polygon Isosceles triangle Definition & Meaning - Merriam-Webster. 
Two triangles are said to be similar, if every angle of one triangle has the same measure as the corresponding angle in the other triangle. The more modern definition of an isosceles is a triangle with at least two equal. The sum of the measures of the three exterior angles (one for each vertex) of any triangle is 360 degrees. The measure of an exterior angle of a triangle is equal to the sum of the measures of the two interior angles that are not adjacent to it this is the exterior angle theorem. An exterior angle of a triangle is an angle that is a linear pair (and hence supplementary) to an interior angle. This allows determination of the measure of the third angle of any triangle, given the measure of two angles. The Merriam-Webster dictionary defines an isosceles triangle as a triangle in which two sides have the same length. Hence, the other side measures the same as given two equal sides, i.e., 4 inches. So, the triangle is not isosceles but equiangular. Solution: We observe that since all the angles measure 60circ. This fact is equivalent to Euclid's parallel postulate. In an isosceles triangle, the equal sides measure 4 inches and all the angles measure 60circ. A strong frame shaped like applies to any zone or belt of minan isosceles triangle, and. The sum of the measures of the interior angles of a triangle in Euclidean space is always 180 degrees. ( Webster ) ( Pryce ) A vein or lode as used in the law V - bob. The measures of the interior angles of the triangle always add up to 180 degrees (same color to point out they are equal). Elementary facts about triangles were presented by Euclid, in books 1–4 of his Elements, written around 300 BC. In rigorous treatments, a triangle is therefore called a 2- simplex (see also Polytope). Triangles are assumed to be two- dimensional plane figures, unless the context provides otherwise (see § Non-planar triangles, below). This is an isosceles right triangle, with the sides AB and AC equal and B measuring 90. Isosceles right triangle: In this triangle, one interior angle measures 90, and the other two angles measure 45 each. A triangle with vertices A, B, and C is denoted △ A B C īasic facts A triangle, showing exterior angle d. Broadly, right triangles can be categorized as: 1. It is one of the basic shapes in geometry.
A triangle is a polygon with three edges and three vertices.
0 kommentar(er)
